POUŽITÍ METODY KONEČNÝCH PRVKŮ PŘI VYŠETŘOVÁNÍ DYNAMIKY KONSTRUKČNÍCH ČÁSTÍ ELEKTRICKÉHO STROJE

Autor : RNDr. B. Madejewski,CSc., Výzkumný ústav elektrických strojů, Brno

Autor instruktivním způsobem uvádí možnost uplatnění metody koneč­ných prvků při návrhu krytu ventilátoru.
Recenzovnla: Doc. Ing. Věra Chalupová, CSc.

Článek je v plném znění  uveden v přiloženém souboru typu PDF – ke stažení ZDE.
Tyto formáty PDF jsou čitelné ve volně dostupném  programu Adobe Acrobat Reader.

1. ÚVOD

Část mechaniky, která se zabývá studiem pohybu fyzikálních systémů působe­ním vnějších sil, se jmenuje dynamika. Jedním z druhů dynamického chování systému je kmitavý pohyb.
Kmitavé pohyby lze rozdělit do dvou základních skupin podle charakteru jejich chování - jde o systémy lineární a nelineární. Pro první z nich platí princip superpozice, který významně zjednoduší postup řešení. Popis a řešení nelineárních problémů je značně komplikovanější a v našich úvahách se jimi nebudeme zabývat. Kmitavý pohyb lze dále rozdělit do dvou základních kategorií - vlastní a vynuce­ný. V obecném případě je nutno, brát v úvahu i příslušné tlumení systému. V pří­spěvku se budeme zabývat podrobně řešením lineárního, vynuceného a tlumeného kmitavého pohybu vyšetřované fyzikální soustavy.

…

3. NUMERICKÁ METODA ŘEŠENÍ

Rešení diferenciálních rovnic určujících spolu s odpovídajícími okrajovými podmínkami fyzikální děje kmitání popsané v předcházející části, je téměř vždy založeno na přibližných metodách. V této souvislosti nutno zdůraznit, že volba typ_ použité přibližné metody má velký význam, a to jak z hlediska přesnosti, tak z hlediska vynaložených nákladů. Jedna z nejužívanějších metod v současné době je právě metoda konečných prvků. Teoretické základy této metody lze formu­lovat na principu virtuální práce nebo lze vycházet z variačního principu ve smyslu minimalizace zvoleného funkcionálu - [3], [8], [9].
Cílem přibližného řešení je redukovat diferenciální rovnici nebo řadu rovnic a příslušné okrajové podmínky na soustavu algebraických rovnic. Z toho důvodu se řešená oblast dělí na řadu prvků a na každém z nich se předpokládá změna určená zvolenou aproximační funkcí. Na hranicích prvků se zvolí jistý počet uzlových bodů, u nichž se předpokládá uskutečnění vazeb se sousedními prvky. Přibližné řešení se hledá na konečně dimenzionálním podprostoru celkového uvažovaného prostoru. Rešení pak lze vyjádřit jako lineární kombinaci konečného počtu bázo­vých funkcí. Příslušné tvary bázových funkcí pro jednorozměrné, dvourozměrné i třírozměrné typy úloh jsou známy - [8], [9].
Uvedená metoda řešení využívající metodu konečných prvků je v podmínkách VÚES Brno realizována programovým souborem TPS 10. Tento programový soubor vyvinula firma T-Program v NSR - [1]; je vypracován v jazyce Fortran IV. Reší rovinné i prostorové úlohy z lineární statiky, nelineární statiky a z dyna­miky, dále řeší potenciální problémy stacionární a nestacionární. Právě posledně uvedené použití představuje řešení teplotních nebo jiných fyzikálních polí, lami­nární proudění, problémy akustiky apod. - [2], [3]. Pro řešení lze použít celkem 17 typů různých prvků; prutové prvky, plošné prvky, roštové, trojúhelníkové a. čtyřúhelníkové. Dále trojúhelníkové a čtyřúhelníkové prvky membránové, deskové a skořepinové a konečně prostorové prvky - tetraedr, pentaedr a hexaedr. Zadání úloh se provádí tak, že je možno použít částečného generování zadávaných dat. Přitom je zajištěna i grafická kontrola zadání. Výsledky výpočtu mimo ta­belárních přehledů lze rovněž zobrazit graficky, což činí uvedený způsob zvláště vhodný pro praxi, neboť obraz umožňuje předání velkého množství informací ve vzájemných souvislostech.
Samotná metoda konečných prvků zpracovaná v uvedeném výpočetním systému spolu s využitím výkonných výpočetních zařízení nabízí v obecnějším smyslu jistý druh stavebnice s daným počtem konečně velkých, geometricky jednoduchých prvků přesně určených vlastností. Z nich lze pak skládat složitější útvary. Takto je možno nahradit skutečný konstrukční dílec. Správnost sestavení prvků v mate­matický model struktury a správnost výpočtu za předem daných podmínek za­jišťuj e výpočetní zařízení a program samotný. Volba struktury modelu s rozdělením na prvky patří do oblasti, v níž se rozvíjejí myšlenkové návyky a zkušenosti pracovníka. Proto je uvedená metoda zvláště vhodná pro řešení inženýrských problémů
a její využívání představuje typický příklad aplikovaného výzkumu. Vyšetřování příčin zvýšeného kmitání a hlučnosti strojů a hledání cest pro jejich snížení patří k případům použití této metody.

4. VYŠETŘOVÁNÍ KMITÁNÍ KRYTU VENTILÁTORU

Jako příklad systematicky vedených výpočtů vlastního i vynuceného kmitání konstrukční části elektrického stroje uvedeme zde přehled vyšetřování krytu ventilátoru malého asynchronního motoru výšky osy H = 80 mm. Cílem výpočtu i experimentu bylo ověřit, zda zeslabení krytu z původní tloušťky d = 1,0 mm na tloušťku d = 0,8 mm nepřinese zhoršení parametrů kmitání a hluku.

4.1. Vlastní frekvence krytu ventilátoru

Základní a výchozí otázkou pro řešení tohoto problému bylo určení vlastních frekvencí obou alternativ krytu ventilátoru. Pro výpočet byla použita metoda konečných prvků, realizovaná výše popsaným programovým souborem TPS 10.
K popisu struktury krytu ventilátoru bylo použito celkem 48 prutových prvků. v rovině Y -Z. Jako další charakteristiky použitých prvků se zadávají plocha průřezu a kvadratický moment průřezu k neutrální ose rovno běžné s rovinou X - Y. Okrajové podmínky jsou simulovány v příslušných bodech upnutí krytu. Uspořá­dání struktury pro popis vyšetřovaného krytu ventilátoru je zřejmé z obr. 1.

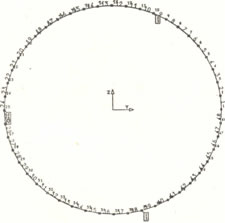
Obr. 1. Struktura popisu krytu ventilátoru pomoci prutových prvků

Z analýzy zadání úlohy byly vytipovány parametry krytu, jež mají vliv na hod­notu vlastních frekvencí.
Jde o následující parametry:
-průměr krytu ventilátoru,
- axiální délka krytu ventilátoru,
- tloušťka krytu ventilátoru,
- místo upevnění krytu ventilátoru,
- způsob upevnění krytu ventilátoru,
- materiál krytu ventilátoru.

První dva z uvedených .parametrů nebyly v našich úvahách měněny. Průměr krytu ventilátoru vzhledem k velikosti motoru není možné měnit a axiální délka krytu vzhledem k požadovaným rozměrům motoru nemůže být rovněž překročena. Tloušťka krytu jako velmi významný parametr byla zadávána pro obě hodnoty d = 1,0 a d = 0,8 mm, odpovídající skutečně vyrobeným krytům.
Výsledky výpočtu prvních pěti vlastních frekvencí krytu při pevném upnutí v místě uchycení krytu na štítu motoru jsou uvedeny v tab. 1 a obr. 2 až 6. Na nich jsou zřejmé tvary vlastních vektorů představujících výchylky krytu, pochopitelně ve zvětšeném měřítku.
Z výsledků je zřejmý výrazný posun ve frekvenčním spektru krytu ventilátoru způsobený změnou parametru tloušťky krytu. Uvedená skutečnost se také po­

Tab. 1. Vlastní frekvence krytu ventilátoru při
pevném uchycení v bodech struktury
10, 25, 39

tvrdila výsledky měření kmitání a hluku obou alternativ na skutečném asynchron­ním motoru.
Další z uvedených parametrů, majících výrazný vliv na hodnotu vlastních frekvencí, tj. místo upevnění krytu ventilátoru, nebyl systematicky vyšetřován. Je to dáno skutečností konstrukčního řešení, u něhož nálitky na štítu motoru určené pro uchycení krytu ventilátoru jsou co do umístění jednoznačně..dány uspo­řádáním žeber na kostře motoru.

Velmi důležitou a početně vyšetřovanou otázkou bylo stanovení vlivu způsobu uchycení krytu ventilátoru na vlastní frekvenci popsané alternativy. Rozumíme tím kombinaci "pevného" uchycení odpovídajícího nulovým posunům struktury ve směru Y a Z a nulovému natočení ve směru X s uchycením "měkkým", které je simulováno pouze nulovým posunem ve směru Y a Z. Početně byla prošetřena řada alternativ možných kombinací těchto uchycení. Dostali jsme tak celou škálu možného frekvenčního složení vlastních kmitočtů těchto uspořádání. Z nich je zřejmé, že způsob uchycení krytu ventilátoru mění výrazně numerickou hodnotu vlastních frekvencí. Pro praxi to znamená, že "přiladění" krytu může být dosaženo již pouze samotným větším či menším přitažením krytu ventilátoru na štít motoru. Výpočet umožní postihnout rovněž alternativu, jestli-že jeden nebo dokonce dva z příchytných šroubů krytu scházejí. Lze tedy tímto způsobem simulovat nejrůz­nější podmínky uchycení krytu ventilátoru. Přitom numerické výsledky jsou vždy doplněny příslušným grafickým vyjádřením tvaru kmitání - [7].
Posledním parametrem, který byl početně vyšetřován, byla materiálová kon­stanta vyrobeného krytu. Lze počítat vlastní frekvence pro materiály navzájem výrazně odlišné svým modulem pružnosti, Poissonovým číslem a hustotou. Tak byl porovnán například ocelový plech, z něhož se kryt ventilátoru běžně vyrábí se sklotextitem. Hodnota vlastní frekvence krytu ventilátoru klesla u druhého z uvedených materiálů přibližně na jednu polovinu a znamená tedy výrazný posun, se kterým je možno v konstrukční praxi počítat - [7].

4.2. Vynucené harmonické kmitám krytu ventilátoru

Programový soubor TPS 10 dovoluje navíc dále provést systematické vyšetřová­ní harmonického buzení daného konstrukčního dílce, v uvažovaném případě tedy krytu ventilátoru. Síly působící toto buzení mohou být například elektromagne­tického původu (výrazný diskrétní charakter frekvenčního složení) nebo aerody­namického původu (spojité frekvenční spektrum). Sestavení úlohy umožní vhodně simulovat charakter budicí síly tím způsobem, že se systematicky mění její zadávací parametry, jimiž jsou:

- místo harmonického buzení,
- amplituda budící síly,
- frekvence budicí síly,
- velikost tlumení konstrukčního dílce,
- fázový posun mezi jednotlivými budicími silami,
- superpozice jednotlivých dílčích zdrojů harmonického buzení.

Jako například uvedených jednoduchých výpočtů uvedeme zde vyšetřování harmonického buzení krytu ventilátoru v jednom jediném místě, označeném ve struktuře krytu ventilátoru na obr. 1 uzlem číslo 1. Směr vektoru budicí síly je radiální, směřující do počátku zvolené souřadnicové soustavy.
Pro jednoduchost jsme pro námi vyšetřovaný případ zvolili amplitudu budicí síly v uvedeném směru rovnu 10 N. Početně byl systematicky sledován vliv budicí frekvence na velikost výchylky vyšetřované struktury. Budicí kmitočet byl zvolen vzhledem k hodnotám první vlastní frekvence krytu ventilátoru uvedené v tab. 1 tak, že dovoloval posoudit velikost odezvy na kmitočtech nižších i vyšších než byla samotná první vlastní frekvence. Konkrétně byl výpočet proveden pro hodno­ty f = 50, 150, 250, 316, 350 a 450 Hz. Grafické výsledky pro vybrané frekvence jsou uvedeny na obr. 7 až 9.

Z výsledků je patrný vliv frekvence budicí síly na vynucené harmonické kmitání krytu ventilátoru. Výrazná je rezonance struktury pro hodnotu prvního vlastního kmitočtu.
Důležitou otázkou je tlumení vyšetřované struktury. To bylo simulováno roz­dílnou hodnotou koeficientu poměrného útlumu δ, což je bezrozměrná veličina definovaná jako poměr součinitele lineárního tlumení a kritického tlumení
δ = b / bk  = b/(2mΩ)
(b je poměr tlumicí síly k rychlosti pohybu tlumené struktury, Ω je kruhová frekvence netlumené struktury, m je hmotnost _struktury). Vliv tlumení struktury byl postupně vyšetřován pro hodnotu koeficientu poměrného útlumu δ = 0,03; 0,1; 0,3; 0,5 a 0,9.
Budicí frekvence pro výpočet byla zvolena totožná s první vlastní frekvencí kry tu ventilátoru. Výsledky vybraných případů jsou uvedeny na obr. 10-12.

Uvedené obrázky dávají dobrý přehled o tom, jaký je vliv tlumení na výchylky vynuceného kmitání krytu ventilátoru. V případě vyšetřování harmonického buze­ní na více místech struktury je možné ve výpočtu respektovat i fázový posun mezi průběhem budicích sil v jednotlivých místech. Velmi důležitou skutečností je i to, že lze provést výpočet buzení v jednotlivých místech struktury (např. pro různé hodnoty budicí frekvence), dílčí výpočty uložit do paměti počítače a potom provést superpozici takto stanovených dílčích složek ve výslednou odezvu uvažované struktury. Případy tohoto typu byly rovněž početně vyšetřovány.

5. ZÁVĚR

V článku jsou uvedeny základy matematického popisu vlastního i vynuceného kmitání uvažované fyzikální soustavy. Řešení je zcela obecné v maticové formě a umožňuje tak popsat libovolný tvar vyšetřované konstrukční části. Stručně jsou nastíněny otázky diskretizace výsledných rovnic pomocí metody konečných prvků i vlastnosti a možnosti použitého výpočetního souboru TPS 10.
V aplikační části je potom podrobně uveden případ systematického početního vyšetřování kmitání krytu ventilátoru asynchronního motoru. Jsou porovnávány výsledky výpočtu vlastní frekvence krytu ventilátoru pro postupně se měnící parametry jeho uspořádání i výsledky případu harmonického buzení pro hodnoty proměnné budicí frekvence, resp. různých hodnot koeficientu poměrného útlumu. Výsledky jsou prezentovány v numerické, ale především v grafické formě.
Použití metody konečných prvků dovoluje posoudit nepoměrně více konstrukčních variant z hlediska hluku a kmitání. Je však nezbytné získané výsledky výpočtu alespoň v několika případech konfrontovat s výsledky experimentu a ověřit si tak jejich spolehlivost.

POUŽITÁ LITERATURA

[I] Uživatelská příručka TPS 10. Metoda konečných prvků (překlad z německého originálu)
VÚES Brno, 1981.
[2] Finite - element - methode in der Praxis, Reutlingen 1979, T -Program GMBH.
[3] Bittnar Z., Řeřicha P.: Metody konečných prvků v dynamice konstrukcí, SNTL, Praha 1981.
[4] Rieger, N. F.: The Relationship Between Finite Element Analysis and Modal Analysis,
Sound and Vibration, January 1986, str. 16-31.
[5] Madejewski B.: Příspěvek k aplikaci metody konečných prvků v technické akustice, TES­
teor. č. 1985, str. 105-109.
[6] Madejewski B.: Využití programového souboru TPS 10 v technické akustice, TES - teor.
č. 1986, str. 87-94.
[7] Madejewski B.: Použití metody konečných prvků při výpočtu vlastních frekvencí částí
elektrických strojů), TES 1988 (v tisku).
[8] Zienkiewicz O. O.: The Finite Element Method in Engineering Science, London 1971.
[9] Kolář V., Kratochvíl J., Leitner F., Ženíšek A.: Výpočet plošných a prostorových konstrukcí metodou konečných prvků SNTL 1972.

THE FINITE ELEMENT METHOD APPLICATION FOR THE INVESTIGATION OF THE DYNAMICS OF CONSTRUCTIONAL PARTS OF THE ELECTRIC MACHINE

RNDr. B. Madejewski, CSc.

The author presents by  the instructive way the possibility of the finite element method application for design of the fan casing.

ANWENDUNG DER METHODE DER FINITELEMENTE BEl DER UNTERSUCHUNG DER KONSTRUKTIONSTEILEDYNAMIK EINER ELEKTROMASCHINE

RNDr. B. Madejewski, CSc.

Der Autor fiihrt aufinstruktive Weise die Anwendungsmoglichkeit der Methode der Finitelemente beim Entwurf des Schutzdeckels eines Ventilators cín.

APPLlCATION DE LA MÉTHODE DES ÉLÉMENTS FINALS POUR L'ÉTUDE DE LA DYNAMIQUE DES PARTIES DE CONSTRUCTION D'UNE MACHINE ÉLECTRIQUE

RNDr. B. Madejewski, CSc.

L'auteur présente la possibilité de l'application de la méthode des éléments fi:q,als au projet du couvercle de protec ti on ďun ventilateur par le mode instructifi